Статистика голосований по странам
Статистика голосований пользователей
Чтобы оставить комментарии, необходимо авторизоваться. За оскорбления и спам - бан.
58 комментариев, показывать
сначала новые
сначала новыесначала старыесначала лучшиеновые - список
Хороший пример оптимизации бизнес-процессов с хорошей коррупционной составляющей.
Или на старорусском: "с миру по нитке - голому рубаха".
+0–
ответить
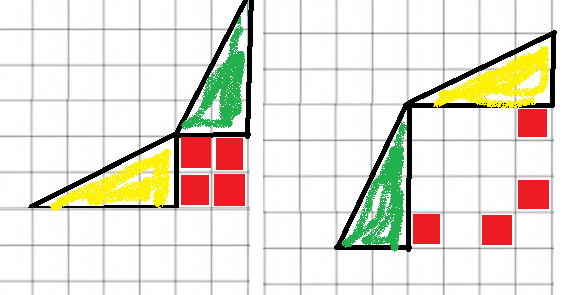
Хорошая оптическая иллюзия. Отношение катетов:
Красный треугольник - 3/8
Зеленый треугольник - 2/5
Так что видимая "гипотенуза" большого треугольника - это не прямая,
а ломаная из двух отрезков.
На вернем рисунке ломаная "выгнута" вниз,
а на нежнем рисунке ломаная "выгнута" вверх
+0–
ответить
lohhersonskii ★• 06.02.25 22:01🇺🇦
Пустая клетка возникла в связи с перестановкой фигур, составляющих верхний прямоугольный треугольник. Площадь нижнего треугольника равна площади верхнего треугольника. Поэтому никакого противоречия, что появилась одна пустая клетка нет.
+0–
ответить
lohhersonskii ★➦Генрих Монт• 07.02.25 08:40🇺🇦
перед тем, как оправить -не перечитывал. НО ПРОВЕРИЛ
+1–
ответить
Soma➦lohhersonskii• 07.02.25 16:54🇷🇺
вы "проверили" то, что изначально ошибочно приняли на веру
нет никакой ложки треугольника вверху, как и внизу
+0–
ответить
Если серьезно, то тангенсы тут и не нужны )))
Смысл конечно то же самый, но это задача из геометрии 8 класса, подобие треугольников. Откуда и следует, что гипотенузы не лежат на одной прямой
==============
Простой пример (рисунок, найти площадь) можно решить по методике 9 класса (формула), а можно 10 (построением)
+2–
ответить
lohhersonskii ★➦Soma• 06.02.25 20:19🇺🇦
У обоих прямоугольных треугольников катеты равны. Следовательно, равны и гипотенузы. Они не лежат на одной прямой, они параллельны
+-1–
ответить
Regerald➦lohhersonskii• 07.02.25 07:00🇫🇮
Отношения катетов друг к другу: 8:3 у красного треугольника, 5:2 у зелёного. Дальше тригонометрия.
+0–
ответить
Soma➦lohhersonskii• 07.02.25 10:18🇷🇺
не совсем понял, про что вы и что сравниваете
в 8 классе методика была бы примерно такова (Углы, образованные секущей параллельных прямых, Соответственные углы, Подобие треугольников):
1. верхний рисунок, проверяется подобие красного треугольника и "большого".
5/13 > 3/8. Подобия нет, значит гипотенузы не на одной прямой, катет большого "треугольника" больше необходимого, "большая гипотенуза" вогнута
2. нижний рисунок (зеленый треугольник и большой) 5/13 < 2/5, катет большого "треугольника" меньше необходимого, "большая гипотенуза" выпукла
+0–
ответить
Soma➦lohhersonskii• 07.02.25 10:31🇷🇺
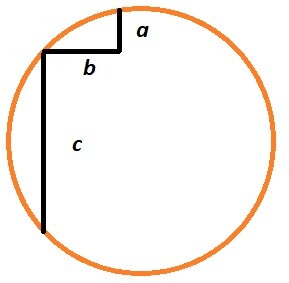
Я потому и привел рисунок примера, что задания всегда имеет множественность решений, но даются именно под конкретную тему (изучаемую в данный момент)
Так, пример на рисунке можно решить геометрически (если таково задание): строим дополнительную хорду, потом из середины строим высоты, пересекающиеся в центре окружности, получаем радиус, откуда и площадь
А можно через относительные координаты и алгебру: локальная система координат в центре окружности (x0=0, y0=0), координаты одной точки примем х, у, тогда другие точки выразятся через x/у и константы a,b,c. Три системы уравнений окружности с тремя неизвестными (x, y, R). Находим R, откуда и площадь.
Все зависит от того, для какой цели дается задание, какова точность вычислений, и какой метод применять. Но всегда решающим оказывается точность создаваемого для описания базиса
+0–
ответить
lohhersonskii ★➦Soma• 07.02.25 14:02🇺🇦
Не буду комментировать весь этот бред. Только отмечу, что термин "вогнутая гипотенуза" в математике не существует
+0–
ответить
lohhersonskii ★➦lohhersonskii• 07.02.25 14:05🇺🇦
также не существует термин "выпуклая гипотенуза".
+0–
ответить
Soma➦lohhersonskii• 07.02.25 14:38🇷🇺
Именно потому и в кавычках, чтоб указать на заблуждение, что большие фигура на обоих рисунках - треугольники, а их мнимая гипотенуза таковой не является. Ведь это и есть самая частая ошибка тех, кто поверхностно анализирует задачу.
Например, вы и сами допустили именно эту ошибку:
lohhersonskii➦Regerald• 07.02.25 08:36
"у обоих треугольников отношение катетов 5:13"
При том, что там нет треугольников с катетами 5:13 и самих катетов, там четырехугольники и их стороны. Вы поверили зрительной оценке и ошиблись с формулировкой исходных данных
Я в кавычки заключал и "треугольник", и "большую гипотенузу", указывая, что это не их математическое определение, а допускаемый статус, предположение
Если быть педантичным, то надо писать "предположим, что это прямоугольный треугольник". И далее - гипотенуза такого треугольника была бы... что невозможно... значит... Метод доказательства от противного. Я просто в несколько раз сократил текст, вырезая наиболее очевидные куски
==============
А вот где вы увидели "бред" - для меня загадка. Я достаточно детально разжевал пример, его в школе любой учитель примет за правильный
+0–
ответить
Soma➦lohhersonskii• 07.02.25 14:46🇷🇺
На всякий случай даже поясню, почему я применял кавычки, видимо вы историю геометрии не знаете
Этимологически слово "гипотенуза" обозначает "натянутый", точнее "натянутый снизу". Почему "снизу"? Тут все просто - один конец нити фиксировался, второй продевался ушко/петлю, а свободный конец нити натягивался грузом, отвесиком. Именно этот способ описан в греческом строительстве и в астрономических приборах (например, первый вариант трикветра)
Соответственно, если нить провисает вниз или топорщится вверх, т.е. отклоняется от натянутого состояния, то слово "гипотенуза" становится неприменимым к такому случаю
+0–
ответить
lohhersonskii ★➦Soma• 07.02.25 15:31🇺🇦
Опять не буду комментировать ваш бред, только прошу ответить, почему вы не прокомментировали моё замечание по поводу "выпуклых" и "вогнутых" гипотенуз?
+0–
ответить
Soma➦lohhersonskii• 07.02.25 16:52🇷🇺
видимо потому, что я то ваш странный вопрос прокомментировал, только вы этого даже не поняли )))
Ну, а если вы не поняли моего комментария, то методика решения таких задач для вас сложна, а винить вас в незнании математики было бы слишком жестоко. Продолжайте считать, что это все волшебство...
Ἀγεωμέτρητος μηδεὶς εἰσίτω
(не заморачивайтесь - считайте, это это заклинание)
+0–
ответить
lohhersonskii ★➦Soma• 07.02.25 17:01🇺🇦
Вместо того, чтобы признать свою ошибку, присвоив термины "выпуклая" и "вогнутая" к гипотенузам, вы извиваетесь в потоке демагогии. Вам требуется помощь психотерапевта.
+0–
ответить
Soma➦lohhersonskii• 07.02.25 17:17🇷🇺
так у меня не было ошибки )))
Я не писал вогнутая гипотенуза, я писал "вогнутая гипотенуза". Вы или невнимательны, или у вас некоторые проблемы с восприятием. Кавычки ("") часто используют для обозначения понятия "так называемая". В устной речи для такого понятия (ложный смысл) так и говорят - в кавычках.
Например - он был тот еще "друг". И это не значит, что речь о друге, по сути речь о том, кого ошибочно записывают в друзья
Перечитайте внимательнее и увидите, что ошибок у меня как раз нет. Если конечно у вас и с русским языком нет сложностей )))
+1–
ответить
Soma➦lohhersonskii• 07.02.25 17:19🇷🇺
Для сравнения, вот у вас была явная ошибка, когда вы четырехугольник назвали треугольником (без кавычек и без пояснений о предположении или допущении)
+0–
ответить
lohhersonskii ★➦Soma• 07.02.25 18:36🇺🇦
Я нигде не называл четырехугольник треугольником. Потрудитесь это показать. Ваше утверждение ложное и только подтверждает, вам нужна помощь психотерапевта.
+0–
ответить
lohhersonskii ★➦Soma• 07.02.25 22:57🇺🇦
Зачем врёшь? В кавычки взята гипотенуза. А "вогнутая" написано без кавычек. То же самое и с "выпуклой".
+0–
ответить
lohhersonskii ★➦Soma• 07.02.25 23:36🇺🇦
Ἀγεωμέτρητος μηδεὶς εἰσίτω в переводе: агометритос Медейс Исифон. Что за очередной бред выставил? Обратись к психотерапевту
+1–
ответить
Soma➦lohhersonskii• 10.02.25 14:02🇷🇺
lohhersonskii➦Soma• 06.02.25 20:19
У обоих прямоугольных треугольников катеты равны.
lohhersonskii➦Regerald• 07.02.25 08:36
у обоих треугольников отношение катетов 5:13.
===============
5 и 13 - в вашем понимании это две стороны треугольников. И вы это упорно повторяли. Вам стыдно это признавать?
======
Я же писал:
катет большого "треугольника" больше необходимого, "большая гипотенуза" вогнута
В кавычки заключал и "треугольник", т.е. указал, что это не треугольник на самом деле и "большую гипотенузу", т.е. это не гипотенуза, и указал, что для этой фигуры данная кривая вогнутая, относительно псевдотреугольника
Повторюсь - перечитайте внимательнее тексты и обдумайте, прежде чем закапывать себя еще глубже
==============
PS Ἀγεωμέτρητος μηδεὶς εἰσίτω - это был слоган над дверью Академии Платона.
Дословно - "негеометр не войдет". Художественно - "нет входа тому, кто не знает геометрию". Повторюсь, не заморачиваетесь )))
+0–
ответить
Soma➦lohhersonskii• 10.02.25 14:07🇷🇺
кстати, тут вас лайкает один безграмотный кадр. Рекомендую и ему для общего развития
https://math.ru/lib/zaochn/4
https://etudes.ru/etudes/gliding-doors/8/
+0–
ответить
lohhersonskii ★➦Soma• 10.02.25 21:58🇺🇦
пишешь чушь. Фантазируешь насчет вогнутости и выпуклости гипотенуз, это же бред, но тебе это нравится. Обратись к психиатру.
+0–
ответить
lohhersonskii ★➦Soma• 10.02.25 22:06🇺🇦
Нахватался ты верхушек, но всё ложное. Фраза "не геометр да не войдет" будет на греческом языке такой:
όχι γεωμέτρης, ας μην μπει. Сомневаюсь, что до тебя это дойдет. Лечись.
+0–
ответить
Soma➦lohhersonskii• 11.02.25 11:13🇷🇺
да что же с вами делать то...
Я не писал о выгнутости гипотенуз, я писал:
Soma➦lohhersonskii• 07.02.25 10:18
..
"большая гипотенуза" вогнута
Еще раз - я не говорил, что гипотенуза может быть выгнута или вогнута, у указал, что кривая, соединяющая две точки и ошибочно называемая (в том числе вами) "гипотенузой" вогнута
===============
Спрошу повторно - вы понимаете смысл применения кавычек? Специально для вас даже процитирую панятие из википедии
"Кавы́чки — парный знак препинания, который употребляется... если они включаются в текст не в своём обычном значении, используются в ироническом смысле..."
Представьте себе, я преступно применил нормы русской пунктуации, которые вас так раздражают )))
==========
По секрету - ваше применение современного греческого для тех времен... советую все же изучать историю
Греки начали писать слева направо только в 4 веке до н.э., но вот старый алфавит продержался долго, причем тогда было 3 основных греческих языка (если брать уже после микенского линейного письма) - Гомеровский, Аттический и Койне.
Да, по секрету - ваше применение запятых умиляет. Первые точки конечно предложил Аристофан Византийский (глава александрийской библиотеки) в 3 веке до н.э., только как их должны были применять когда не только библиотеки, но даже Александра не существовало еще? )))
===========
К слову, на современном греческом пишут сейчас "Μηδείς αγεωμέτρητος εισίτω"
https://www.alfavita.gr/koinonia/451235_ti-simainei-i-frasi-mideis-ageometritos-eisito
Обращайтесь к реальным источникам, а не онлайн-переводчикам )))
+0–
ответить
Soma➦lohhersonskii• 12.02.25 10:36🇷🇺
т.е вы даже после "пАнятнее" не поняли юмора и искали ошибку в "вас"?
увы, это действительно тяжелый случай )
+-1–
ответить
lohhersonskii ★➦Soma• 12.02.25 12:21🇺🇦
Общаться с тобой - зря тратить время. Твой очередной высер только подтверждает мой вывод
+0–
ответить
Soma➦lohhersonskii• 12.02.25 12:37🇷🇺
не со мной тебе надо "общаться", а учить школьные курсы математики и русского )))
+0–
ответить
Soma➦lohhersonskii• 12.02.25 12:39🇷🇺
заметь - ты с самого начала хамишь, но даже сам не осознаешь, что этим сам же себя и показываешь быдлом )))
+0–
ответить
Генрих Монт ★• 06.02.25 16:05🇷🇺
Наконец-то! Фокус-покус публикован там, где количество знаков на ответ не ограничено. Получите!
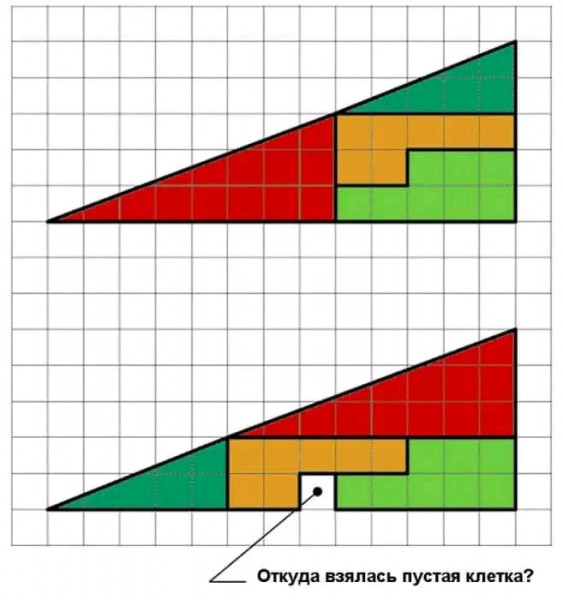
Первое, что я вычислил, - это общую площадь большого треугольника и сумму площадей фигур, его составляющих .
Здесь было обнаружено первое несоответствие. Площадь большого треугольника оказалось равной =32,5 кв.ед., тогда как сумма площадей равна 12+8+7+5=32 кв.ед. За единицу измерения принята сторона клетки на рисунке.
Сумма площадей фигур на нижнем рисунке (вместе с квадратом) равна 33 кв.ед. Это притом, что площадь большого треугольника остается 32,5.
Тогда я осторожно предположил, что большие фигуры могут являться не треугольниками, а четырехугольниками.
Исходя из того, что оба малых треугольника прямоугольные, вывел тангенсы их наиболее острых углов. Они оказались равными 0,4 и 0,375. Из чего сделал однозначный вывод, что при различных тангенсах могут быть только различные углы.
Но, так как моих оппонентов даже это не убедило, то, естественно, и в меня закрались сомнения. Тогда решил высчитать гипотенузу большого треугольника и сумму гипотенуз красного и зеленого. Чтобы сравнить.
Гипотенуза большого треугольника оказалась равна = 13,928388277.
Гипотенуза красного треугольника оказалась равна = 8,544003745.
Гипотенуза зеленого треугольника оказалась равна = 5,385164807.
То есть сумма гипотенуз малых треугольников, равная 13,929168552, отличается от большой гипотенузы приблизительно на 0,00078028. Расхождение, вроде, ничтожное, но оно есть. Значит, большой верхний треугольник состоит не из четырех, а из пяти фигур. Есть еще и очень тупоугольный треугольник.
И последнее, что предпринял, – так это, зная длину трех сторон, вычислил площадь предполагаемой мною фигуры по формуле Герона.
Она (площадь) оказалась равной 0,50000 кв.ед. Именно так, с точностью до пятого знака. Из всего вышеизложенного мною был сделан вывод об обмане зрения. На верхнем рисунке мифической гипотенузой добавляется 0,5 кв.ед., на нижнем же гипотенузой 0,5 кв.ед вырезается, но добавлен квадратик в 1 кв.ед.
+24–
ответить
Ю ★★★➦Генрих Монт• 06.02.25 16:08🇺🇦
Медаль "Король перфекционистов" с закруткой на спине этому человеку!!
+16–
ответить
Генрих Монт ★➦Ю• 06.02.25 16:24🇷🇺
"Если уж делать, то по-большому!" (приписывается Л.И. Брежневу)
+4–
ответить
CAHTEXHuK➦Генрих Монт• 06.02.25 20:17🇱🇻
Мошно задвинул, но ответ про 5 пустых клеток лучше и понятен третьекласнику
+1–
ответить
Olesia➦Генрих Монт• 07.02.25 08:18🇺🇸
на верхнем убирается, на нижнем добавляется место в большом треугольнике его гипотенузой
+0–
ответить
а вот в СССР в школе была миллиметровка! если на ней нарисовать тонким карандашом, глупые вопросы бы не появлялись. ах да, еще надо гипотенузу большого треугольника нарисовать, линейкой! :)
+4–
ответить
Хренонимус ★• 06.02.25 15:07🇱🇻
- Нужно приложить линейку;
- Из-за изменения суммарной толщины линий;
По чуть-чуть набирается.
Те, кто плитку клали - знают ;)
+6–
ответить
Красный треугольник, соотношение катетов 8/3 = 2,6(6); площадь 12 кл.
Зелёный треугольник – 5/2 = 2,5; площадь 5 кл.
Общая площадь фигур = 12+5+7+8 = 32 клетки (верхний рисунок).
----------------------
Суммарный (якобы) треугольник – 13/5 = 2,6
При прямой гипотенузе площадь должна быть 32,5.
Реально нарисована площадь 32+1 = 33 клетки.
+8–
ответить
Генрих Монт ★➦Гарик О• 06.02.25 18:53🇷🇺
Я себе это представляю.
Учитель: "Здравствуйте, дети, садитесь. Сегодня мы будем проходить... что? Правильно, Гарик О, эту наёбку!"
+2–
ответить
Гарик О ★➦Генрих Монт• 06.02.25 19:04🇷🇺
примерно так
только вместо наёбки было что-то другое )))
+0–
ответить
И если посмотреть на гипотенузу сбоку, то видно, что на верхнем рисунке она выпуклая, а на нижнем вогнутая.
+7–
ответить
Ю ★★★• 06.02.25 13:13🇺🇦
Мля, та сколько уже можно? "Гипотенуза" 1-го треугольника - на самом деле не отрезок, а ломаная. Ну то есть, у красного и зелёного треугольников тангенсы разные. 3 : 8 ≠ 2 : 5. В общем, кому надо, тот понял.
+11–
ответить
62_Alexandr➦Ю• 06.02.25 13:32🇷🇺
Вообще то тангенс не у треугольников а у углов, но по сути верно. Кроме этого даже без тангенсов видно что углы разные, достаточно посмотреть на 4 клетку от левого угла.
+3–
ответить