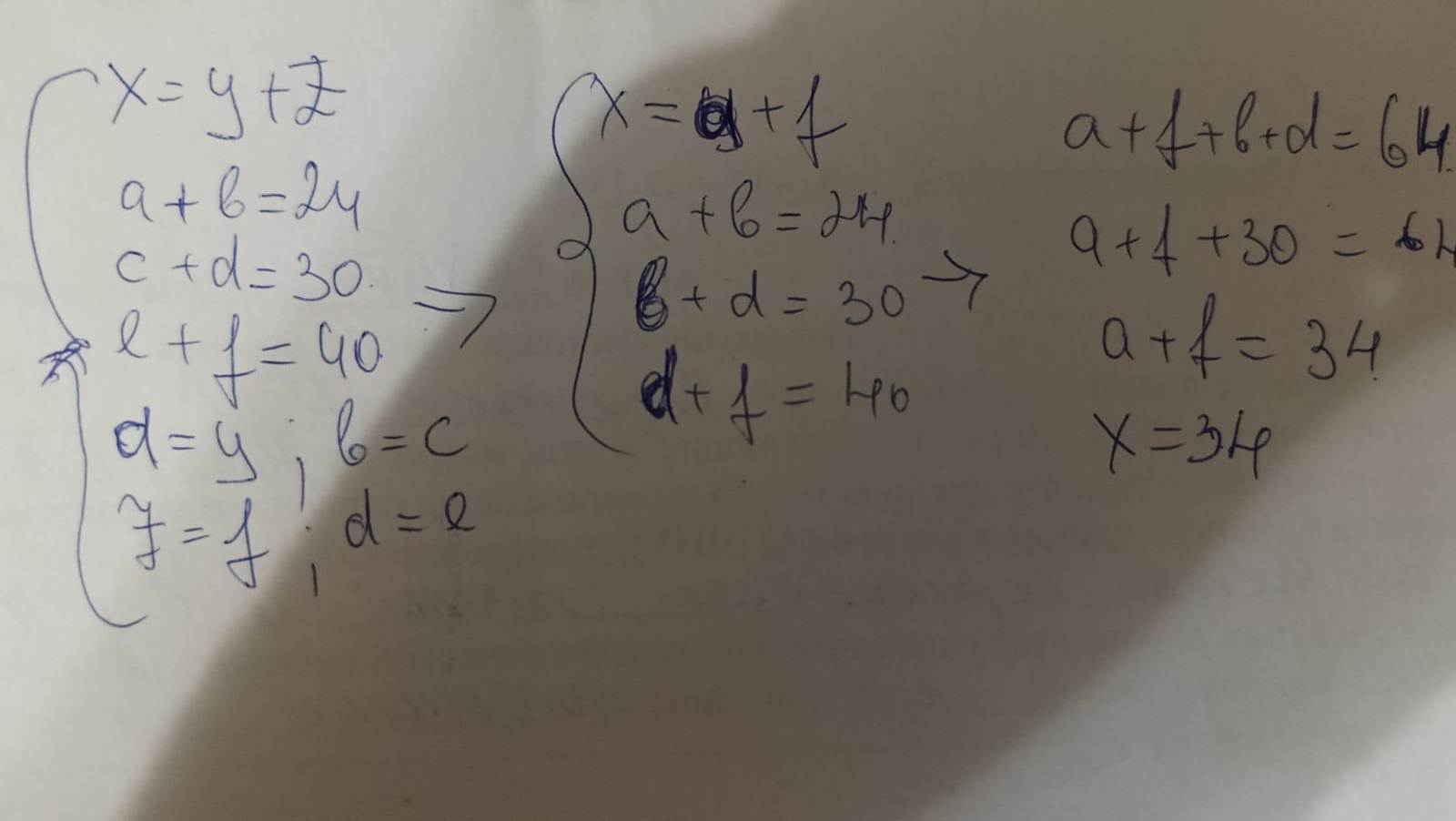Статистика голосований по странам
Статистика голосований пользователей
Чтобы оставить комментарии, необходимо авторизоваться. За оскорбления и спам - бан.
46 комментариев, показывать
сначала новые
сначала новыесначала старыесначала лучшиеновые - список
Разделим квадрат на четыре части. Пусть площадь четвертинок s. Площади треугольников, показанных на рисунке, совпадают (одинаковые основания и высоты). Пусть это будут a и b. Тогда площади, заданные в условии:
s-a-b = 24
s+b-a = 30
s+a+b = 40
s+a-b = ?
Складывая первое и третье, получаем 2s=64, или s=32, а площадь всего квадрата 128. Отсюда недостающая площадь x = 128-24-30-40 = 34.
Второй вариант - если 32+b-a=30, то a-b=2 и 32+a-b=34
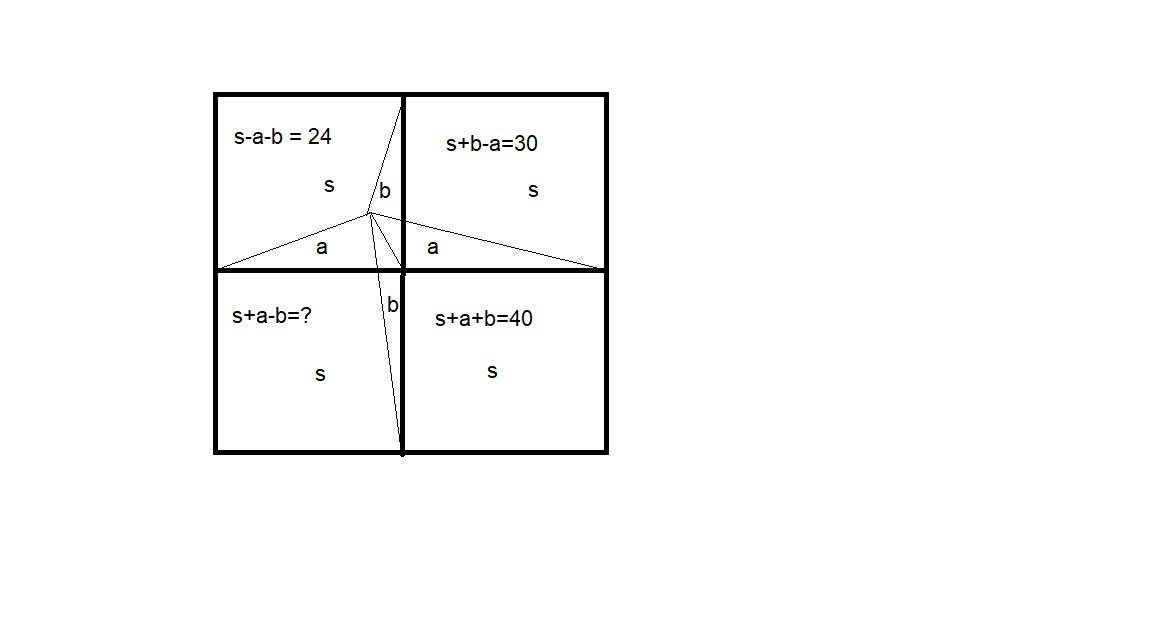
+3–
ответить
34. Площади треугольников равны, если равны их основания и опущенные на них высоты. А дальше обычная линейная алгебра и подстановки
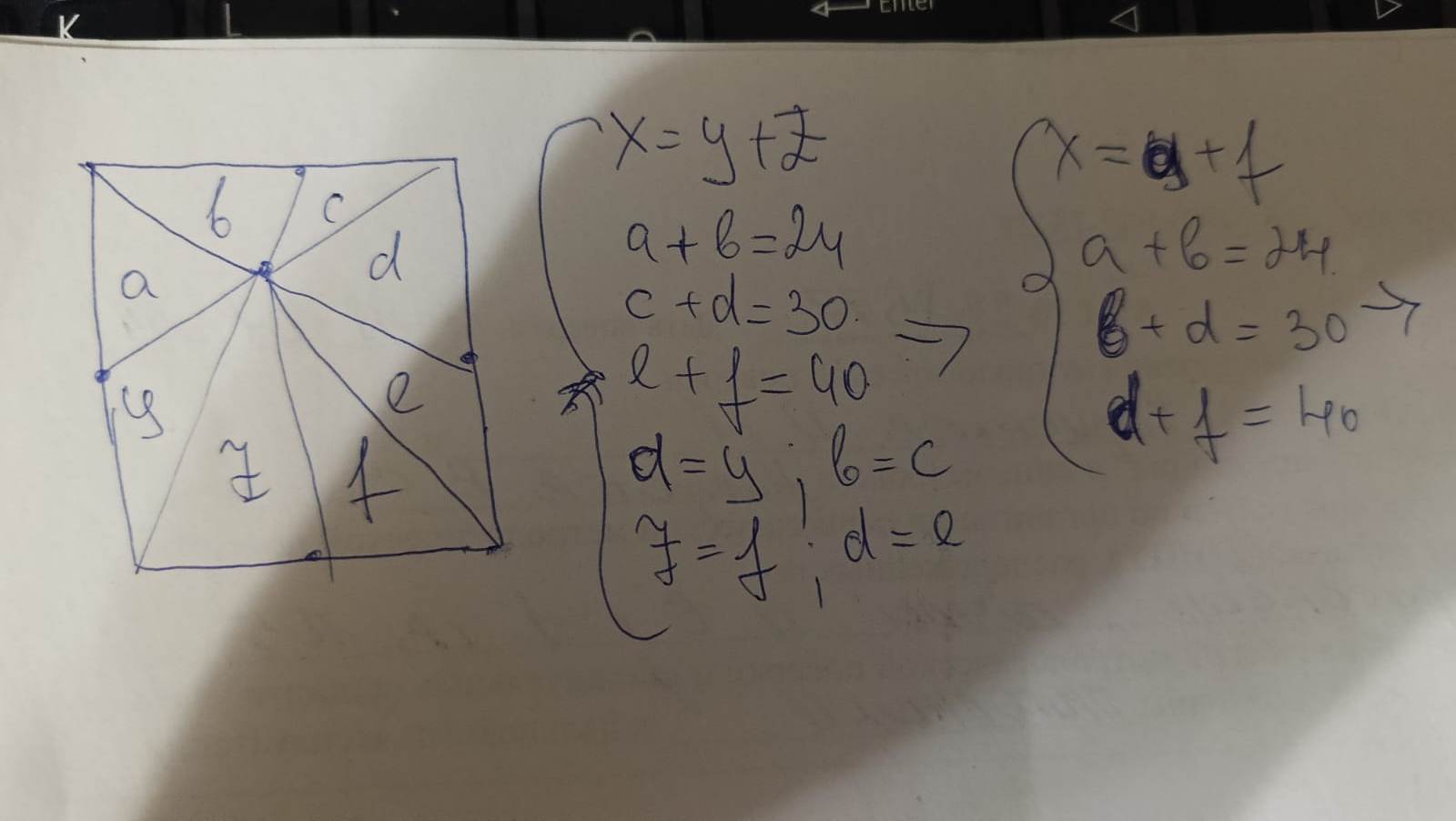
+5–
ответить
Здесь и вычислять ничего не надо: X = 30. ТОчка внутри квадрата лежит на его диагонали, она же ось симметрии. Следовательно четырёхугольник X - есть отражение четырёхугольника 30, т.е. они равны. Как следствие - равны их площади
+0–
ответить
ginger_ape➦kamakama• 26.03.25 21:09🇷🇺
На всякого мудреца довольно простоты... если глазомер не развит, проведите диагональ и можете убедиться сами.
+-1–
ответить
kamakama ★➦ginger_ape• 26.03.25 21:16🇷🇺
Причем тут глазомер? Вы это докажите, как положено. Как в школе теорему доказывают. Более того, от положения этой точки на диагонали или нет ответ ВООБЩЕ не зависит
+2–
ответить
ginger_ape➦kamakama• 27.03.25 11:56🇺🇸
Видимо с геометрией туго. Как раз если точка на диагонали лежит то всё просто. В противном случае тоже просто: X = 34
+-1–
ответить
kamakama ★➦ginger_ape• 27.03.25 14:51🇷🇺
Смешной. То есть если лежит, то 30. А если не лежит, то 34 (откуда кстати эта величина?). Докажи))) Я вот выше посчитал и доказал, строго как положено
+1–
ответить
Другой ник➦Pepper• 26.03.25 16:15🇷🇺
Правильно, но очень много вычислений. Проводим отрезки через все середины сторон, получаем квадрат, разделённый на 4 треугольника. Проводим из общей вершины высоты. Они лежат на двух перпендикулярных отрезках, (поскольку стороны попарно параллельны). Эти два отрезка, перпендикулярные отрезки равны по длине, поэтому две пары площадей треугольников, имеют равные площади. Следовательно, суммы площадей противолежащих четырёхугольников равны. Отсюда 40+24-30=34.
Опускаем высоту на
+4–
ответить
Смотрите:
1. стороны у квадрата равны, об этом говорят двойные черточки на сторонах.
2. Чисто визуально видно, что точка вообще не симметрична ничему.
3. Чтобы площади были целыми, тогда и стороны должны быть целыми. Правда, теоретически именно площадь последней фигуры (X) может быть не целой, тогда и стороны квадрата будут с десятичными дробями. Но если мы все-таки говорим о целых числах, тогда ближайщие длины квадрата 11 и 12см.
4. Если взять 11см, то площадь всего квадрата = 121, тогда х = 27, что близко к истине. А если взять сторону квадрата 12см, то площадь всего квадрата равна 144, а Х=50, что чисто визуально никак не может быть.
Я понимаю, что мое доказательство ненаучно, но я уверен, что Х = 27
+1–
ответить
Krotik➦Krotik• 26.03.25 14:17🇷🇺
когда я писал выше, что 27 близко к истине, я имел в виду визуально
+0–
ответить
demontag➦Krotik• 26.03.25 15:14🇷🇺
«Сколько будет ноль целых пять десятых плюс одна вторая?». А я нутром чую, что литр, но математически доказать не могу!
+6–
ответить
Krotik➦ioger• 26.03.25 15:20🇷🇺
ну я про это и пишу, вообще-то.
Вы, наверное, большой начальник, если так хорошо умеете выслушать чужую идею и тут же преподнести ее как свою?
+0–
ответить
Генрих Монт ★➦Krotik• 26.03.25 16:34🇷🇺
"Чтобы площади были целыми, тогда и стороны должны быть целыми"
Откуда вы это взяли? Мой привет вашей учительнице по математике. Площадь квадрата может быть равна и 35, и 34, и 33. И даже 11,3137084989.
+2–
ответить
Lepan ★• 26.03.25 14:04🇷🇺
Без уточнений не подлежит решению. Точка, которая лежит внутри прямоугольника, вовсе не обязательно расположена равноудаленно от сторон.
+-2–
ответить
Генрих Монт ★➦Lepan• 26.03.25 14:18🇷🇺
Всё подлежит
https://dzen.ru/a/Xu-XYXtYWQhxPh_P?ysclid=m8ptrknc2e158686286
+2–
ответить
30, красавцы, 30 (тридцать): это же симметрично с противоположным!
+-1–
ответить
Генрих Монт ★• 26.03.25 13:24🇷🇺
34, сколько же ещё?
На геометрию ходить надо было, а не письками за гаражами мериться
+4–
ответить
Генрих Монт ★➦demontag• 26.03.25 14:18🇷🇺
Подвело вас чувство. 34 правильный ответ
https://dzen.ru/a/Xu-XYXtYWQhxPh_P?ysclid=m8ptrknc2e158686286
+0–
ответить
Krotik➦Генрих Монт• 26.03.25 14:45🇷🇺
я почитал, автор там бред пишет. и другие комментаторы по Вашей ссылке со мной согласны.
Теперь рассмотрим Ваш ответ. 24+30+40+34 = 128 площадь всего квадрата.
И что - сторона квадрата = корень из 128 равна 11,3137084989.... дальше кончилась разрядность калькулятора? Это бред сивой кобылы. А вот мой ответ ниже вполне логичен
+-2–
ответить
Генрих Монт ★➦Krotik• 26.03.25 16:38🇷🇺
Кротик, если бы Ленин был с вами знаком, он "учиться" повторил бы четыре раза.
Визуально он решает геометрические задачи...
+4–
ответить
Генрих Монт ★➦ssskkk• 26.03.25 14:17🇷🇺
возмоно, очень даже возмоно
https://dzen.ru/a/Xu-XYXtYWQhxPh_P?ysclid=m8ptrknc2e158686286
+1–
ответить