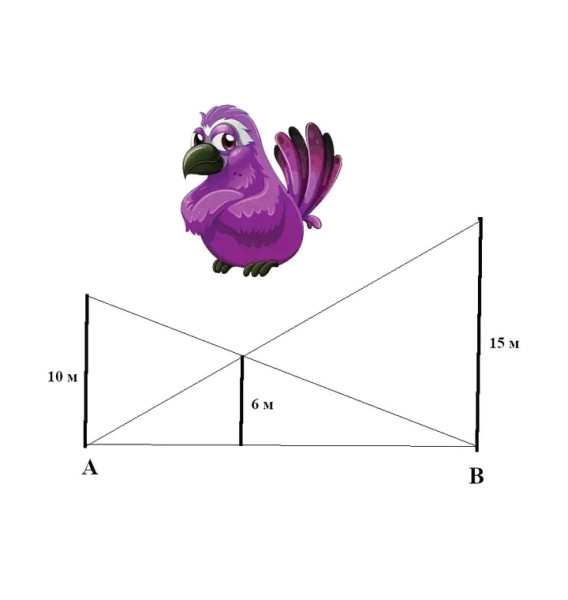
Чему равно расстояние AB ?

Задача для настоящих джедаев. 😉 Бессмысленная и беспощадная капча супротив DeepSeek и примкнувшего к нему ChatGPT. 😉
Всё просто. Расстояние от А до В равно расстоянию от В до А. Докажите что я не прав?
Мне удалось убедить ChatGpt. Когда я попросил доказать, что АВ не может быть равен 5, он нарисовал картинку, на которой катерты пересекаютсмя на высоте ровно 6 и заявил: "Верёвки (наклонные линии) пересекаются не на высоте 6 м, а выше." КОгда я возразил, он сказал, что "Я просто поставил точку на 6 м, как будто они там пересекаются, вручную" . И лишь когда он просчитал точку пересечения на координатной плоскости, то согласился: "Ты был абсолютно прав:
Если предположить, что AB = 5, то пропорции соблюдаются и пересечение действительно происходит на 6 м.
А значит, AB не вычисляется однозначно из высот палок и высоты пересечения без дополнительных условий.
Если хочешь, я могу переписать полное аккуратное решение задачи с правильным выводом:
AB может быть любым, если горизонтальные отрезки x и y относятся как 3:2." ChatGpt не только конкретно ошибается, но и еще с упорством настаивает на ошибочном решении. :)
AntuanDE➦Коммутатор• 26.05.25 22:54🇷🇺
Почему? Ноль тоже подходит. Будут три вертикальных линии исходящих из одной точки. Отрезок от верхней вершины "левой" линии в точку B тоже будет вертикальным и пересечет верхнюю вершину средней линии. Так что 0 - включительно.
Soma➦AntuanDE• 27.05.25 14:10🇷🇺
0 включать нельзя, т.к. однозначно не выполнится отношение деления основания как 2 к 3, там точка неопределенности, к которой может только стремиться
Оби Ван Киноби ★★★• 26.05.25 15:13🇲🇩
Фокус в том, что чат GPT решил эту задачу, а Google Gemeni не смог. И написал, что чат GPT ошибается :)
Derrick➦Оби Ван Киноби• 26.05.25 16:31🇬🇪
Мне он на русском в первом же абзаце выдал полную чушь (у него бывает):
На изображении показаны два прямоугольных треугольника с общей горизонтальной стороной между точками A и B, а также высоты к этой стороне: одна из левого треугольника — 10 м, другая из правого — 15 м. Также дан отрезок между высотами — 6 м.
И продолжил:
Левый треугольник:
Высота: 10 м
Горизонтальный катет: 6 м
10 метров это катет, но 6 м - нет.
Derrick➦Derrick• 26.05.25 16:32🇬🇪
А, вру, перепутал. Это как раз ChatGPT такую фигню прогнал. Gemini правильно написал, что информации недостаточно.
Не хватает данных. Минимальное решение в натуральных числах - пять. В целых - 0.
Так что, еще будут данные? Пока что бесконечное число решений.
Как далеко не отдаляй стойку B, пересечение будет на высоте 6, а отношение АС к BC как 2 к 3. Но таких вариантов множество
Данных недостаточно. Картинку можно растягивать и сжимать в горизонтальной плоскости, не меняя длины вертикальных линий.Треугольники при этом останутся треугольниками, но длина AB изменится.
papavitya➦СанитарЖеня• 26.05.25 21:06🇷🇺
Для этого и есть второе условие – 6 м от горизонтального катета до точки пересечения.
Abondarev➦papavitya• 27.05.25 00:20🇷🇺
Это условие ничего не даёт. Если вкопать вертикально столб высотой 10 метров, затем на любом расстоянии от него столб 15 метров, затем соединить их двумя проводами от макушки одного до подножия другого, то провода всегда пересекутся на высоте 6 метров. На плоской Земле и при непровисающих проводах, разумеется. Это легко доказать через подобие треугольников, и как пишется в хороших книгах по математике, доказательство предоставляется читателю ))
Soma➦papavitya• 27.05.25 14:05🇷🇺
Там прикол в подобии треугольников (больших и малых). Средняя вертикальная линия делит основание на 2 к 3, как сильно не разделять точки А и B
Если кратко, все что дает нам такое условие:
1. обозначим верхние точки вертикалей Е над А, F над C и D над B.
2. укажем тангенсы углов DAB и EBA через "большие" и "меленькие" треугольники
tg DAB = tg FAC = FC/AC = DB/AB
tg EBA = tg FBC = FC/BC = EA/AB
тут FC = 6, DB = 15, EA = 10. АB = AC+BC
из двух уравнений выразим AB:
3. подставим и найдем отношение AC к BC
6/AС = 15/AB, AB = 15/6 AC = 5/2 AC
6/BС = 10/AB, AB = 10/6 AC = 5/3 BC
тогда 5/2 AC = 5/3 ВС, или 3*АС=2*ВС, соответственно АB = АС+ВС = AC + 3/2AC = BC + 2/3 BC
=========================
Вот в общем и все, что получится определить. Если нужны целые величины допустимых AB,то они кратны 5: 2+3, 4+6, 6+9, 8+12...
Soma➦papavitya• 27.05.25 14:38🇷🇺
кстати, автор мог бы продлить задачу и дальше, тогда было бы намного интереснее.
Если левую вертикаль (от точки А) сдвигать влево, до положения А1, когда вертикальный отрезок станет равен не 10, а 15 (т.е. как и отрезок над точкой В), отрезок АА1 окажется равен половине АВ.
И тогда можно на основе такого простого примера прийти к золотому сечению